 Basıklık (Kurtosis) Örnekleri
Basıklık (Kurtosis) Örnekleri
Sıfırdan tepeye, tepeden tepeye ve RMS gibi nicel metriklere ek olarak, bir dalga formu sinyalinin şekline ilişkin metrikler çıkarmak da mümkündür.
Dijital bir sinyal zaman içinde ayrık noktalardan oluştuğu için, herhangi bir titreşim sinyalini ivme noktalarının istatistiksel bir dağılımı olarak ele alabiliriz.
Titreşim sinyalleri ve Gauss Eğrisi
Muhtemelen normal ya da Gauss dağılımını duymuşsunuzdur. Bu, doğal olayları modellemek için en yaygın kullanılan olasılık dağılımlarından biridir.
Aşağıdaki şekil incelendiğinde, bu dağılımın 3 sigmaya karşılık gelen en geniş aralığı, bir sinyalin değerlerinin yaklaşık %99,74'ünü temsil etmektedir. Bu bölge, sürecin doğal değişim aralığı olarak bilinir.

İstatistikte, bir sürecin her zaman belirli bir değişkenlik derecesine sahip olduğu, yani belirli bir varyasyonla bir değerler aralığında çalıştığı anlaşılmaktadır. Süreç istikrarlıysa, bu, varyasyonun bu değerler aralığında gerçekleşeceği anlamına gelir.
Bu kavramı makine titreşimine uygularsak, ivmelenmede rastgele bir sinyalimiz varsa, aşağıdakine benzer bir normal dağılıma sahip olacağız:


Basıklık (Kurtosis)
Kurtosis metrikleri (bozulma olarak da çevrilir) önemli bir istatistiksel parametredir. Bu parametre, bir titreşim sinyalinin şeklini niteliksel olarak tanımlamak için kullanılır.
Titreşim analizi bağlamında bu parametre, bir sinyalin tepe noktalarının yanı sıra ortalama değeri etrafındaki simetri derecesini ölçmek için kullanılır.
Bir titreşim sinyalindeki basıklık, soldaki şekilde gösterildiği gibi sinyal değerlerinin dağılımına bakılarak grafiksel olarak yorumlanabilir.
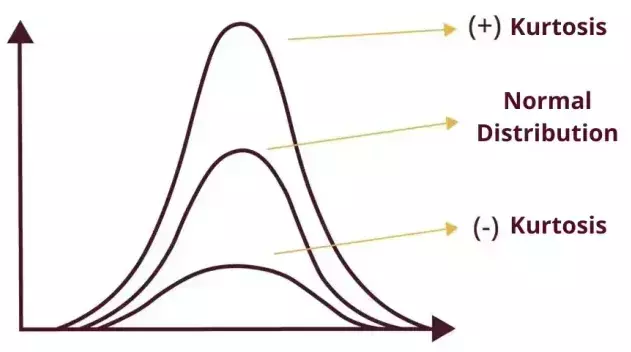
Normal veya rastgele dağılıma sahip bir sinyalin dağılım şekli, daha önce gösterildiği gibi, 3'e eşit bir basıklık değerine sahiptir.
Daha yüksek basıklığa sahip bir dağılım, ortalaması etrafında yoğunlaşan değerlerle daha konik bir şekle sahip olacaktır. Öte yandan, daha düşük basıklığa sahip bir dağılım, değerlerin daha geniş bir aralığa yayıldığı düz bir şekle sahip olacaktır.
Kısaca basıklık, bir sinyalin değerlerinin ne kadar benzer olduğunu ifade eder. Bu nedenle, çok sayıda farklı tepe noktası veya darbe içeren bir sinyal olması durumunda basıklık daha yüksek olacaktır.
Şimdi bazı örneklere bakalım:
Yeni bir rulmanda, kusur olmaması nedeniyle, aşağıdaki dalga formunda gösterildiği gibi oldukça rastgele bir sinyal beklenir. Bu durumda, basıklık değeri 3'e yakın olacaktır.


Bir rulmandaki kusurlar ortaya çıktıkça ve geliştikçe, darbe sinyalleri sinyal dağılımını doğrudan değiştirir, bu da basıklık değerinde bir değişikliğe yol açar. Aşağıda görebileceğimiz gibi, sinyal 10 gibi yüksek bir basıklık değerine sahiptir.

Her durumda, dalga biçiminden ivme, hız, yer değiştirme ve zarf açısından basıklığı çıkarmak mümkündür, bu da analizi daha zengin ve daha uygun hale getirir.
Daha fazla basıklık uygulaması örneği
Zaman karşılaştırmaları kusur gelişimlerini tanımlamak için de geçerlidir. Aşağıdaki örnekte, aşağıdaki spektral zarfta gösterildiği gibi, bir rulman kusuru (iç yuva) olan titreşimli bir eleğin uyarıcısını ele alalım:

Bu izleme noktası için zaman ivmesinde basıklık metriğine baktığımızda, yüksek frekans bandına (1000 Hz ila 6400 Hz) odaklanarak değerin önemli ölçüde arttığını görüyoruz. Rulman arızası geliştikçe, dalga formu sinyalindeki tepe noktalarının varlığının arttığını fark edebiliriz.

Bu dalga biçimi parametrelerinin spektral analizin yerini almadığını, aslında tamamlayıcı olduklarını vurgulamak önemlidir. Bu nedenle en iyi titreşim analizi, daha iyi bir teşhis için tüm tekniklerin çaprazlanmasıyla yapılacaktır.

